基于FPGA的移位寄存器流水线结构FFT处理器设计与实现

    对于N点序列x(N)，其傅里叶变换

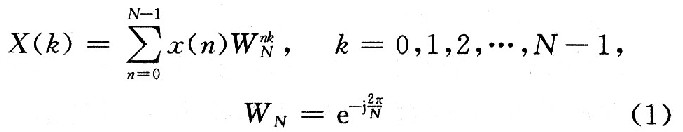
    将x(n)分成上、下两部分，得：
   
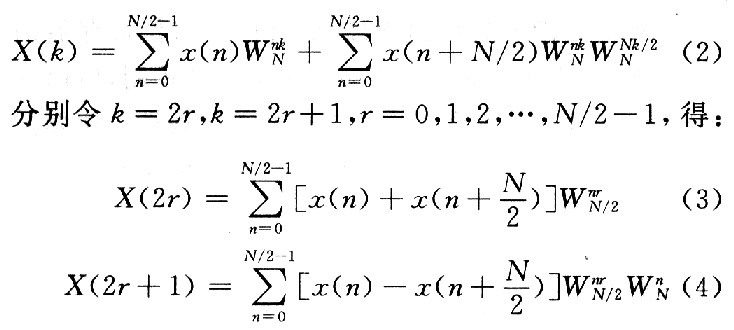
    这样将两个N点的DFT分成两个N／2点的DFT，分的方法是将x(k)按序号k的奇、偶分开。通过这种方式继续分下去，直到得到两点的DFT。采用DIF方法设计的FFT，其输入是正序，输出是按照奇偶分开的倒序。

2 移位寄存器流水线结构的FFT
    在传统流水线结构的FFT中，需要将全部数据输入寄存器后，可开始蝶形运算。在基-2 DIF算法中可以发现，当前N／2个数据进入寄存器后，运算便可以开始，此后进入的第N／2+1个数据与寄存器第一个数据进行蝶形运算，以此类推。
    由于采用频域抽取法，不需要对输入的数据进行倒序处理，简化了地址控制，这样，可以采用移位寄存器的方式，依次将前N／2个数据移入移位寄存器，在N／2+l时刻，第一个数据移出移位寄存器，参与运算。相对于传统的RAM读写方式，采用移位寄存器存储结构综合后的最大工作频率为500 MHz，远大于RAM方式的166 MHz。
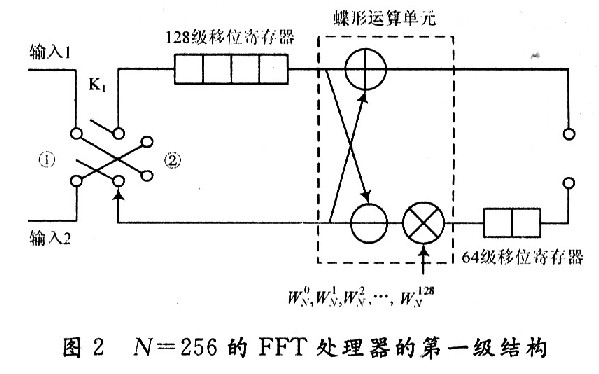
    当移位寄存器相继有数据移出时，在移位寄存器中会出现空白位。此时，引入第二路数据，在第一路数据依次移出进行蝶算时，第二路数据依次补充到移位寄存器的空白位中，为运算做准备。通过这样一种类似“乒乓操作”的结构，可以使蝶形运算模块中的数据不间断地输入，运算效率达到100％。不同于传统的“乒乓操作”结构，由于使用移位寄存器，不需要两块RAM，可以省掉一半的寄存器。图2为256点FFT处理器的第一级结构。

    基于上述基本原理，将这种移位寄存器结构扩展到整个FFT系统的各级，可以发现各级使用的移位寄存器数量是递减的。现使用一个8点结构来进行说明。
    如图3所示，数据由输入l和输入2进入第一级。通过开关进行选通控制。由于是N=8的运算，所以各级分别加入4级、2级和1级的移位寄存器。

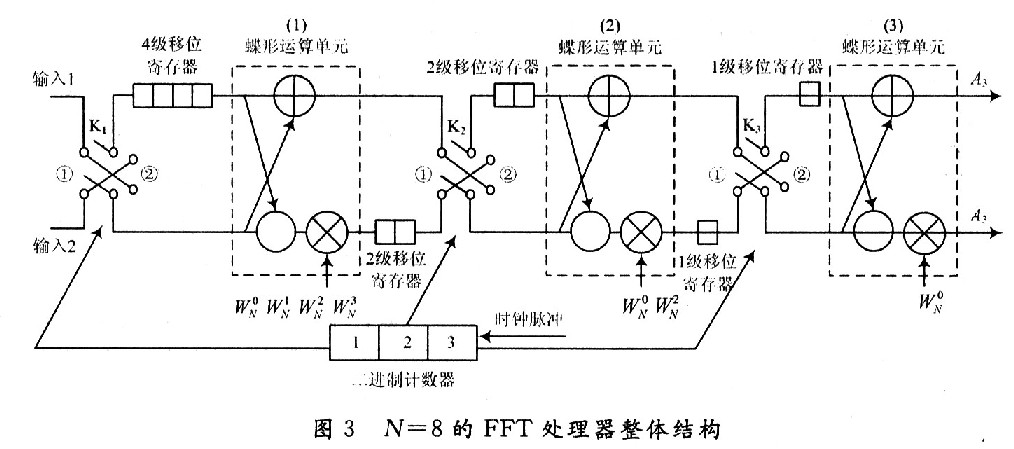
    分两路来说明运算过程：
    将K1打到位置①，第一路数据进入移位寄存器，待第一路的前4个数据存入4级移位寄存器后，第一路进入的第5个数据与移位寄存器移出的第1个数据进行蝶形运算。
    由于输出结果有上下两路，第二级是一个四点的DFT，所以对于上路的输出结果x0(0)+x0(4)类似于第一级，直接存入下一级寄存器，为四点运算做准备，下路的输出，先存入本级2级移位寄存器中，等到上路的四点运算开始，第二级的移位寄存器有空白位时，移入第二级，为下路的四点运算做准备。所以第一级蝶形运算上路输出前N／4=2个进入下一级寄存器，下路输出的数据依次存入本级移位寄存器中。
    当第一级的输出前N／4=2个数据x0(0)+x0(4)和x0(1)+x0(5)存入第二级移位寄存器时，运算便可以开始，这时开关K2打到位置②，此时第一级上路输出的数据x0(2)+x0(6)，即第一级上路输出的第三个数据与第二级移位寄存器移出的第一个数据，即x0(O)+x0(4)进行蝶形运算，输出的第四个数据x0(3)+x0(7)与x0(1)+x0(5)进行蝶算。在这个运算过程中，第一级的2级移位寄存器移出数据依次移位存入到第二级的移位寄存器产生的空白位中。
    两个时钟后，第一级上路输出的四个数据完成了蝶形运算，K2打到位置①，在接下来的两个时钟里，第一级中2级移位寄存器的输出依次与此时第二级中2级移位寄存器的输出数据进行蝶形运算，即与，与完成第一级下路输出的四个数据的蝶形运算。
    此时，第一路在第一级运算后的输出数据，在第二级完成了全部的蝶形运算。第二级的输出结果同第一级一样，蝶形运算的上路输出前N／8=1个进入下一级寄存器，后一个数据直接进入后一级进行碟算，下路输出的数据存入本级移位寄存器中。
    第三级的运算与第二级和第一级类似，即移入1级寄存器的数据与其后一个数据进行碟算，同时使前一级寄存器的输出数据进入后一级寄存器的空白位中，然后开关打到位置②，对下路输出数据进行碟算。
    对于第二路数据，通过开关控制，在第二级中，待第一路第一级下路输出数据进行蝶形运算时，移入寄存器的空白位，为运算做准备，由于前级运算周期是后级运周期的两倍，对于第二级碟算模块而言，数据仍然是不间断输入的。通过这样两路数据的交替运算和存储，实现“乒乓操作”，从而提高了蝶形运算模块的运算效率。图4是256点FFT的具体运算输入和输出时序图。对于只有一路数据的应用场合，可以在前级加入，门控开关和数据缓冲寄存器分成两路数据，实现一路数据的不间断读入。

    由于采用移位寄存器结梅，各级寄存器使用的数量都是固定的，即为N／2+N／4。其中，N为该级DFT运算的点数，各级使用的移位寄存器深度逐级递减，从而大大降低了寄存器的使用数量。
    此外，由于各级结构固定，所以大点数FFT只是小点数FFT基础上级数的增加，而且由于移位寄存器的输出相对于RAM而言不需要复杂的地址控制，所以这种结构的FFT处理器具有非常好的可扩展性。比如需要实现512点的FFT，只需要在256点的基础上增加一级即可。

3 具体模块的设计
3．1 控制与地址产生模块
    由于两路数据同时输入，为了防止发生两路数据间的串扰，对数据的控制显得极其关键。从上面的算法结构分析中知道，由于后级的DFT运算点数是前一级的一半，所以后一级的开关转换周期也是前一级的一半，基于这种关系，可以使用一个8位计数器的每一位状态来对各级开关进行控制。最高位控制第一级，同时由于上一级数据进入下一级需要一个时钟，所以下一级的开关转换时刻要比上一级延迟一个时钟周期。

    对于移位寄存器，在实现时，各级的前级移位寄存器深度为N／2-1，从本质而言，是使运算开始的时钟上升沿到来时，数据已经出现在碟算模块输入线上，而不需要下一个时钟的驱动来移出寄存器，比如第二级移位寄存器的级数为63。这样，运算周期正好是2的倍数，从而方便使用计数器的各位直接对开关进行控制。
    同时，计数器还可以用来产生所需旋转因子的RAM地址。根据各级蝶形运算所需旋转因子的规律，可以利用计数器的高位补零来产生查找表的地址。比如，对于第一级，因为需要在最低位第一次出现1时提供，第二次出现1时提供，…，以此类推，周期为128，所以可以使用计数器的低七位作为地址。对于第二级，由于所需要的地址为偶数，可以由计数器的[6：1]和最低位置O产生。表l为8点时使用三位计数器输出旋转因子的地址情况。

    控制和地址产生模块的仿真结果如图5所示，其中sel代表开关控制，addr代表产生的地址。

3．2 蝶形运算模块
    蝶算模块由一个复数加法器，一个复数减法器和一个旋转因子的复数乘法器构成，如图6所示。

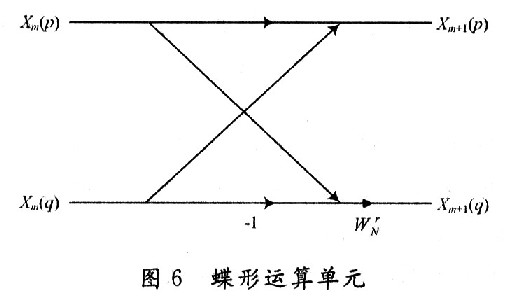
    旋转因子乘法器通常由4次实数乘法和2次加／减法运算实现，但因为cos和sin的值可以预先存储，通过下面的算法可以简化复数乘法器：
    （1）存储如下三个系数：C，C+S，C-S
    （2）计算：E=X-Y和Z=C*E=C*（X-Y）
    （3）用R=（C-S）*Y+Z，I=（C+S）*X-Z，
得到需要的结果。
    这种算法使用了3次乘法，1次加法和2次减法，但是需要使用存储3个表的ROM资源。
    设计中数据的输入为16位复数，所以将旋转因子cos(2kπ／N)，sin(2kπ／N)量化成带符号数的16位二进制数后，存储到ROM中，由于值域不同，需要注意C+S和C-S的表要比C表多1位精度。
    运算后的结果需要除以量化时乘以的倍数16b011111llllllllll。具体实现时由于除法运算在FPGA器件需要消耗较多的资源，设计中采用二进制数移位的方法来实现除法运算。为了防止数据溢出，设计对输出结果除以2。图7为蝶形运算模块的RTL级结构图。

3．3 倒序输出模块
    由频域抽取的基-2算法可知，运算结果需要倒序输出。可以先将结果存储到RAM中，然后使用O～255的二进制数倒序产生RAM读取地址，依次将结果读出，其中实现一个8位二进制数倒序的算法如下：
    (1)将8位数字的相邻两位交换位置；
    (2)将相邻的两位看作1组，相邻两组交换位置；
    (3)将相邻的4位看作1组，相邻两组交换位置。
    经过这样的交换位置后，输出即为原来8位二进制数的倒序。
    举例对于8位二进制数10110110来说，第一次交换位置的结果是01111001，第二次交换位置的结果是11010110，最后交换位置的结果是01101101。可见正好是原来数字的倒序。
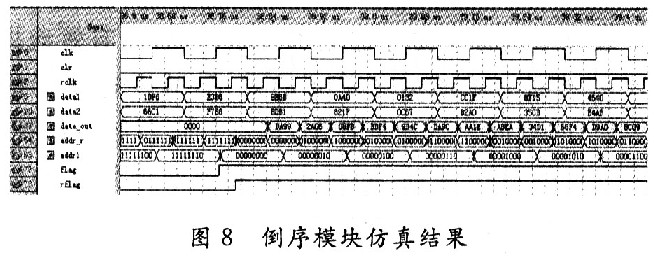
    另外，由于设计的是两路数据同时写入，一路数据读出，所以读取的频率是写入频率的2倍，使用PLL实现原始时钟的二倍频，用来读取RAM。倒序模块仿真结果如图8所示。

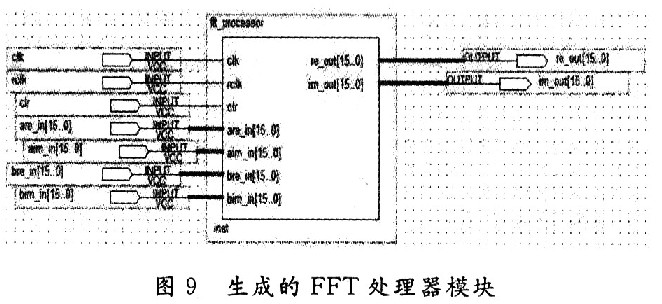
    最终生成的FFT处理器模块图如图9所示。

4 仿真结果
    各级间数据时序情况如图10所示，设计的FFT处理器仿真结果如图1l所示。采用一路阶梯递增信号和另一路：XXXX信号进行仿真，通过与Matlab计算结果进行对比，结果基本一致，可以满足系统要求。系统总的延时由延时最大的第一级决定，为第一级运算的延时加上倒序输出的延时，总共是(256+128)×clk，相对于一般流水线结构(256×读入周期+7×128×蝶算周期+128×读入周期)，系统延时大为减少。

    通过仿真可知，系统最大频率由蝶形运算模块的最大工作频率决定。使用QuartusⅡ软件时序仿真后，得到处理器的工作频率为72 MHz。

5 结语
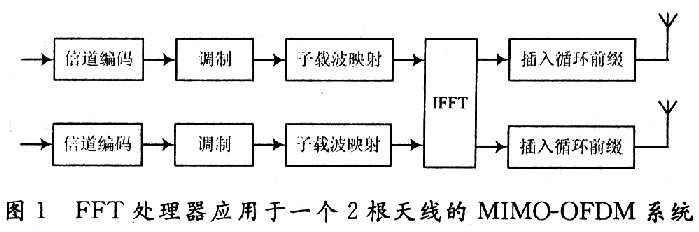
    通过采用移位寄存器流水线结构，可以有效地提高FFT处理器中蝶形运算单元的效率，减少寄存器的使用数量，并且简化了地址控制，提高处理器的工作频率，具有良好的可扩展性，同时可以实现两路数据的同时输入，从而增大了一倍的数据吞吐量。对于工作频率要求较高，数据吞吐量较大，尤其对于需要两路数据输入的场合，比如两天线的MIMO-OFDM系统，具有很大的实用价值。