采用FPGA实现多种类型的数字信号处理滤波器

滤波器是任何信号处理系统的关键组成部分，随着现代应用的日趋复杂，滤波器设计的复杂程度也日益提高。采用 FPGA 设计和实现的高性能滤波器的能力是模拟方法所望尘莫及的。另外，采用FPGA 设计的数字滤波器可以避免模拟设计中存在的某些问题，特别是组件漂移和容差（在高可靠应用中，由温度过高、老化和辐射问题造成）。这些模拟问题会显著降低滤波器的性能，特别是在通带纹波等方面。

当然， 数字模型也有自身的缺陷。滤波器数学运算中的舍入可能会带来问题，因为舍入误差会被累加，给性能造成不良影响，比如增大滤波器的噪声基底。工程师可以采取多种方法最大程度地减轻这种影响，例如使用收敛舍入可以获得比传统舍入更好的性能。最终， 舍入误差问题的严重性与模拟器件相比得到了显著降低。

将 FPGA 作为滤波器构建模块的主要优势之一在于，如果因为集成原因或者需求变动原因需要调整性能，允许在设计过程的后期修改或者更新滤波器的参数，且产生的影响很小。

滤波器类型和拓扑结构

大多数熟知数字信号处理的工程师都知道滤波器的主要类型有四种。低通滤波器只允许频率低于预设截止频率的信号通过。高通滤波器与低通滤波器相反，只允许频率高于截止频率的信号通过。带通滤波器只允许频率在预设带宽内的信号通过，不允许其它频率的信号通过。带阻滤波器与带通滤波器相反，不允许频率在预设带宽内的信号通过，但允许其它频率的信号通过。

大多数数字滤波器都采用下列两种方法之一来实现： 有限脉冲响应(FIR) 和无限脉冲响应 (IIR)。首先我们深入探讨如何设计和实现 FIR 滤波器。这种滤波器也常被称为窗口 sinc滤波器。

为什么我们首先以 FIR 滤波器为重点呢？两种滤波器的最大区别在于有无反馈。对未采用反馈的 FIR 滤波器，在给定的输入响应下，滤波器的输出最终会稳定为 0。而对采用反馈的IIR 滤波器，在相同的给定输入下，输出不会稳定为 0。

FIR 滤波器的设计由于未采用反馈，故天生具有稳定性，因为滤波器的所有极点都与原点重合。IIR 滤波器就没有这么幸运。由于在设计 IIR 滤波器的时候，必须精心考虑其稳定性，这样窗口 sinc 滤波器对新接触 DSP 技术的工程师来说，更加易于理解和实现。

如果要求工程师绘制理想低通滤波器在频域中的原理框图，大多数工程师会画出和图 1 一样的图。

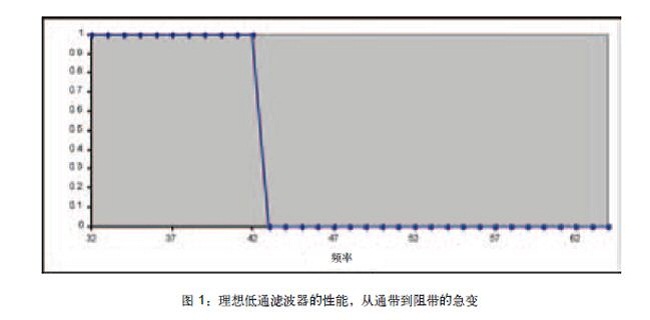
图 1 所示的频率响应一般称为“砖墙型”滤波器。这是因为通带和阻带之间的过渡非常陡峭，要比现实中能够实现的陡峭很多。这种频率响应还具备其它“理想”特性，例如没有通带波纹以及具有理想的阻带衰减。

如果将该图围绕 0 Hz 进行对称扩展，同时扩展到 +/- FS Hz（FS 指采样频率），然后对响应进行离散傅里叶逆变换 (IDFT)，就可以得到该滤波器的脉冲响应，如图 2 所示。

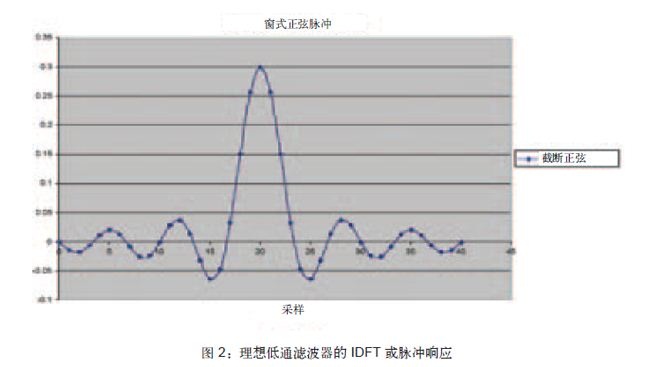
这就是图 1 所示理想滤波器频率响应的时域表示法，也称为滤波器内核。FIR 或窗口 sinc 滤波器正是由这个响应而得名，因为画出 sinc 函数的曲线可以得到脉冲响应：

结合滤波器阶跃响应， 频率响应、脉冲响应和阶跃响应提供了有关滤波器性能的所有信息，可用于判断滤波器是否满足设计要求。