高速移动下OFDM均衡器的FPGA实现

O 引言
   正交频分复用(OFDM)是一种正交多载波调制技术，它将宽带频率选择性衰落信道转换成一系列窄带平坦衰落信道，在克服信道多径衰落所引起的码间干扰，实现高数据传输等方面具有独特的优势。但是由于OFDM信号频谱重叠，对信道变化很敏感，在高速移动下，信道的时变特性更加明显，此时OFDM系统载波间的正交性会遭到破坏，出现载波间干扰(ICI)，这会导致系统性能明显降低。为了消除ICI，必须采用适当的均衡技术以补偿ICI。国内外许多学者对这些问题进行了大量的研究，提出了各种不同的方法，得到了一些阶段性成果。文献提出了一种低复杂度的迭代MMSE均衡器算法，在保证均衡效果的同时把运算量成功降低到o(N)，为该均衡器算法的实际运用奠定了基础。
    现场可编程门阵列(Field Programmable GateArray，FPGA)器件近年来取得了飞速的发展，已经具有强大的计算性能和逻辑实现能力。特别是Xilinx公司的FPGA具有丰富的IP资源，容量大且具有强大的软件支持，在各个领域得到了广泛的应用。本文主要讨论基于Xilinx公司Virtex-2FPGA硬件平台的均衡器算法中矩阵求逆的运算过程实现。将程序下载到FPGA，并通过RS 232将结果数据回送到主机查看和验证。

1 时变信道中OFDM系统均衡器
1．1 时变信道中的OFDM系统结构
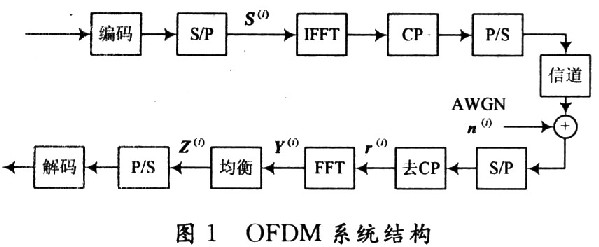
    考虑一个载波数为N的OFDM系统如图1所示，假设完全同步，并且有足够长(不小于信道阶数)的循环前缀(CP)。在去除了循环前缀CP以后第i个数据帧收到的数据矢量为：

   
式中：是OFDM第i个数据帧的输出数据矢量；为N点快速傅里叶逆变换矩阵；，n(i)为信道噪声矢量，定义方差是σ2的高斯白噪声(AWGN)；H(i)是一个N×N的时域转移矩阵，其元素为，其中h(i)(k,n)是描述信道特性的冲击响应。在接收端，对r(i)进行N点快速傅里叶变换，其输出为：
   
式中：
    由于在高速移动的环境下，接收信号会受到ICI的影响，故在整个系统中添加均衡模块，假设均衡器用E(i)来表示，则均衡后的信号可以表示为：
   
1．2 MMSE均衡器算法
    把上面式中的i去掉，根据最小均方误差的规则，可以简写得到均衡矩阵为：
   
   在时变信道中，G不是对角矩阵，则矩阵求逆的直接算法的运算量为o(N3)，利用文献给出的结论：ICI主要来自相邻的几个子载波，并且每个子载波的符号能量主要泄漏至邻近的少数子载波上，也就是说，G中的很大一部分元素是可以忽略的。然后再采用迭代的方法对矩阵求逆，把运算量降为o(N2)，但是在实际应用中，N是一个较大的数值，这个方法计算量仍然很大，所以很多算法在考虑均衡效果的同时也尽量减少运算量，以增强算法的可实现性和最终均衡的实时性。
    根据Chen等验证得到G可以被进一步简化成如下Ak来描述：
   
式中：pn是一个由构成的1×(2Q+1)的矩阵，i=O，1，…，2Q。MMSE均衡器可以描述为；γ为该信道的信噪比，且。Ak是一个(2Q+1)×(4Q+1)的矩阵，再利用文献中迭代的方法来计算矩阵的逆。对于一个OFDM模块来说，该算法的总计算量是o((2Q+1)2N)，由于Q<<N，所以整个计算的复杂度就降低了很多。

2 均衡器算法的FPGA实现
    当载波数比较大时，OFDM均衡算法所要计算的矩阵比较庞大，计算量大，很难保证实时性的要求。于是人们很自然地会想到用实时性很强的FPGA来实现均衡器的设计，但是均衡本身所需要处理的数据量和运算量都非常大，即使使用FPGA实现也很困难。
   若采用文献中的算法运算量是o(N2)，假如当载波数N=128时，运算量还是很大的，无法保证实时性。从均衡效果和运算量两方面考虑，采用了文献中的算法。这是一种典型的迭代算法，效果与文献算法相接近，但是在计算中避免了求一个很大的矩阵的逆运算，而是从频域转移矩阵G中提取出了不大的有效矩阵，这样就减少了大量运算。
2．1 硬件设计思想
    在对均衡器算法进行FPGA设计之前，先用Matlab仿真该均衡器浮点算法，通过分析程序可以发现，该算法的核心部分是迭代求逆矩阵的过程。该算法的瓶颈主要是求解由复数元素组成的矩阵的逆的计算量巨大，而且是浮点数会占用很大的存储空间。为尽量减少需要使用的逻辑资源，在进行ISE设计时，数据用16位定点数表示，其中高8位是整数部分，低8位是小数部分。
2．1．1 硬件设计框图
    实现该均衡器的硬件设计框图如图2所示，其中G为从Matlab中产生的频域转移矩阵，控制模块完成从G中取出对应的有效值得到Ak，并且控制当一组运算完成后运用上一组产生的。进行下一组运算，CIR是该算法的核心，即矩阵迭代求逆的运算，CPE模块是一个简单的矩阵运算模块完成的运算。

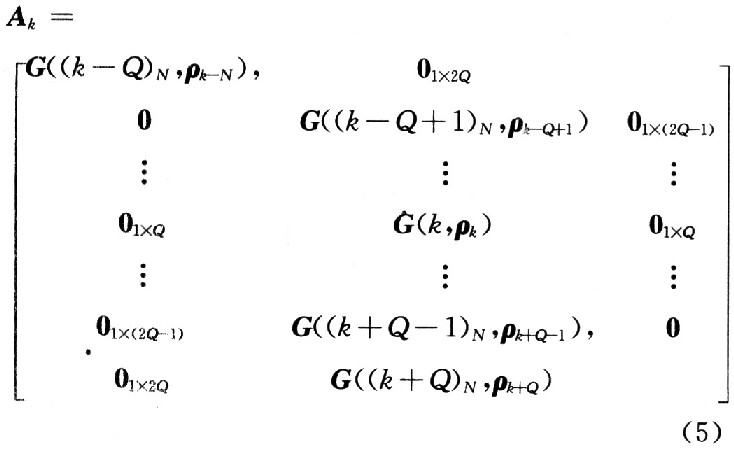
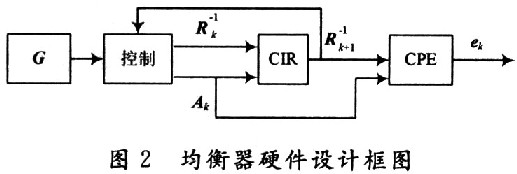
2．1．2 CIR模块介绍
    CIR模块完成矩阵迭代运算过程，它从输入端口读入Ak以及对应的，采用迭代的方法计算出，用FPGA实现这个模块的端口如图3所示。

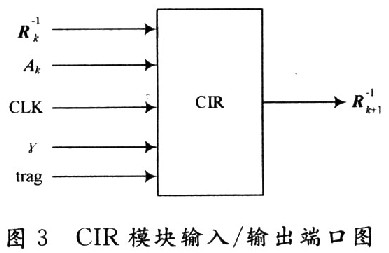
    其中，CLK为时钟；γ是模拟信道的信噪比；Ak是频域转移矩阵G中取出的有效矩阵；trag是控制信号，当一次运算结束产生一个有效的后，只有trag被置为高电平才会进行下一次运算。取Q=2时，是一个5×5的矩阵。整个求逆矩阵的迭代过程就是从前一个5×5的逆矩阵(即)和从频域转移矩阵G中对应区域取得的5×9的矩阵Ak运算出下一个5×5逆矩阵(即)的过程。
   分析其矩阵求逆的迭代算法可以发现，其中大部分完成的是复数矩阵的乘加运算，所有数据是复数，虽然复杂很多，但是实际运算中有许多是多余的。Rk是共轭对称矩阵，上三角部分和下三角部分的实部相同，虚部也只是正负相反，所以只需要算出上三角矩阵的数据，下三角的部分直接对虚部取反就可以了。
   Xilinx的FPGA芯片中集成了硬核的乘加器DSP48，可以方便、高速地进行乘加运算。但是本算法中涉及到的复数运算比较灵活，还包括一些减法运算，直接使用DSP48不是很方便的控制。故设计了一种乘加器，使用了乘法器的IPCore，按照要求设置输入输出数据位数，其中的一个乘加运算中设置乘法器的两路输入为8位，输出为16位，调用IPCore如下所示，算法中其他的矩阵运算也都与此类似。
   
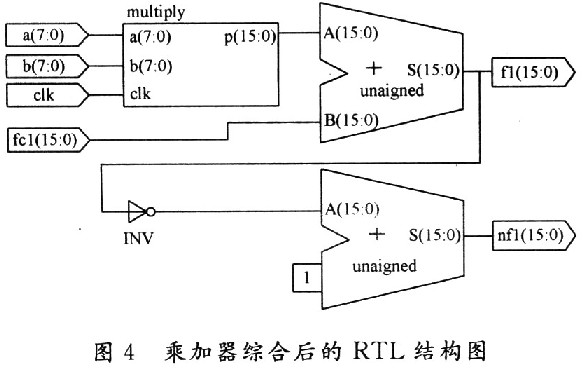
   a，b作为两个寄存器储存参与运算的数据，outl是乘法器计算的结果，用fcl进行存放，相累加得到f1，再按照共轭复数运算的规律得到nfl。实现一个8位×8位的乘加器共消耗了56个Slice，32个LUT和49个IOB。该乘加器综合后的RTL结构图如图4所示。

    为了能最大限度地提高运算速度，所有数据都用可编程逻辑单元构成的分布式存储器存储并列存储，并且根据算法的要求实现的是多个乘加器同时运算，这样虽然使用了很多逻辑资源，但任何数据都可以即取即用，便于进行大量的并行运算，以提高运算速度。
2．2 系统验证仿真
   本系统采用Xilinx公司Virtex-2实验板进行仿真验证，该实验板采用的是XC2VP30芯片，它有30816个逻辑单元，136个18位乘法器，2 448 KbRAM，资源丰富。开发软件为该公司的集成开发软件平台ISE9．2，HDL语言采用Verilog，使用Matlab辅助ISE完成FPGA设计的方法。通过实验板上的RS232串口与PC机进行通信，用Matlab从计算机中传输数据到FPGA芯片中，运算后再通过串口回传均衡后的信号数据到Matlab中仿真验证星座图，以判断该均衡器的效果。

2．2．1 均衡过程
   CIR中使用迭代算法避免了并行大向量和大矩阵的运算，而是分步运算。所以对输入信号进行均衡，首先要进行并串变换，但是不需要变成真正的串行信号。当Q=2时，实际上对需要均衡的输入信号Y(i)每次取出5个数据，用yk表示，暂且将这样的变换叫作分组并串变换(P／GS)，然后均衡矩阵ek与yk分组完成乘法运算得到一个zk，zk是一个数据不是向量，最后进行串并变换就得到均衡后的信号向量Z(i)。整个均衡的过程如图5所示。

2．2．2 仿真结果
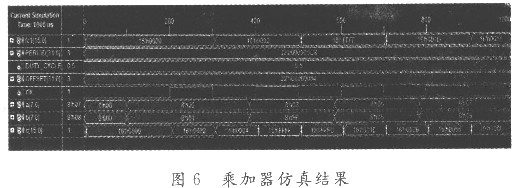
    实现该算法的重要一步是所设计的乘加器可以正常使用，并且实时性好。对其进行仿真如图6所示，可以发现当clk发生上升沿跳变时进行计算，图中信号(a，b)表示输入的数据信号；fcl表示相乘的结果；c表示进行乘加以后的运算结果，其计算准确，基本上没有延迟。

   ISE中设计的传输模块实现波特率为19 200 b／s的串口通信控制器，把数据通过RS232完成FPGA与PC机的双向通信。把均衡后的信号Z(i)传回Matlab中，采用QPSK的星座图进行分析，选择子载波的数目N=128，循环前缀CP的长度为8，并且在认为信噪比被准确估计的情况下均衡的结果，如图7所示。

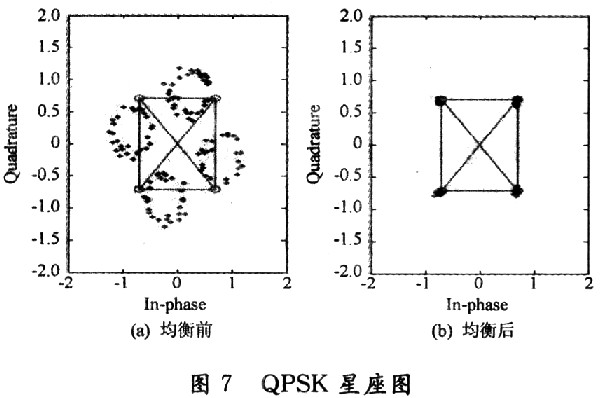
    由此星座图可以看出，在均衡前接收到的信号因为多普勒频移和噪声的影响，偏离星座点向周围发散，使用FPGA中均衡以后传回的数据基本没有发散现象。

3 结语
   在ISE软件平台上使用Verilog语言实现了一种基于时变OFDM系统的低复杂度MMSE均衡器算法。在Xilinx公司Virtex-2实验板(XC2V930芯片)上对其进行验证，基本达到该算法在Matlab上仿真的均衡效果。但是由于浮点数计算量太大，选用定点数对其进行截取，还是有一定的局限性，在进行大量数据的运算中还是会有些数据不太准确，造成整体的误码率效果不是太好，故还需要进一步改进算法和FPGA的实现方法，以期达到更好的均衡效果。