【赛灵思中国通讯54期】利用Xilinx FPGA实现高效并行实时上采样

本文介绍一种使用Virtex-6器件和免费WebPACK工具实现实时四倍上采样的方法。

许多信号处理应用都需要进行上采样。从概念上讲，对数据向量进行M倍上采样的最简单方法是用实际频率分量数的(M-1)倍个零填充数据向量的离散傅里叶变换(DFT)[1]，然后将零填充向量转换回时域[1,2]。但这种方法计算量很大，因此不能在FPGA内部高效实现。在本文介绍的高效并行实时上采样电路中，每个ADC时钟可产生M个上采样值，其中M是所需的上采样倍数。在我们赛灵思的Virtex®-6 XC6VLX75T FPGA实现方案中，上采样倍数M为4，可以作为较普遍方法的一个实例。

我们并行上采样方法的总体概念源于某些作者所称的“窗口SINC插值”，这种方法在文献资料[3,4]中有一些非常精彩的专文介绍。

为了更好的说明，现以图1中所示的16MHz模拟信号为例。该信号的表达式为：

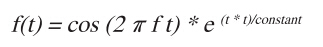
等式 1

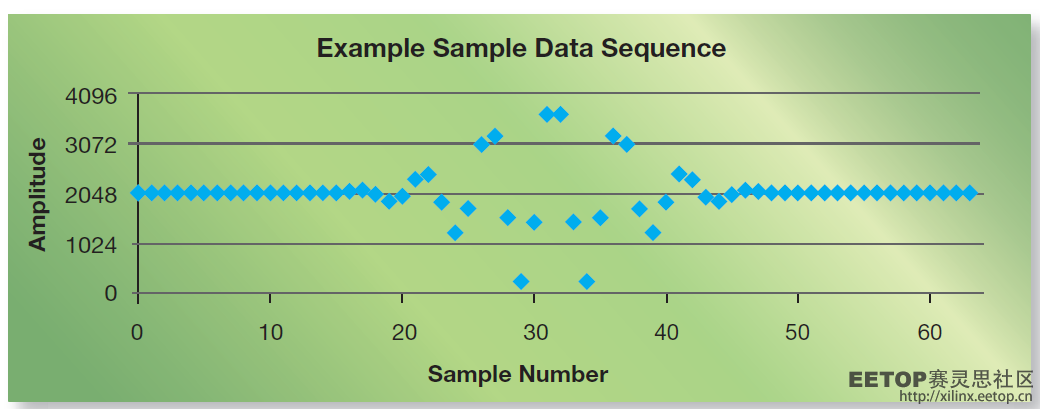
如果用12位ADC以80MHz的频率对图1所示的信号进行采样或量化，输入范围为ADC完整输入范围的97.7%，则每个信号周期只能采样五次，产生的样本数据序列如图2所示。如果对该示例数据序列进行四倍上采样，则有效采样率为320MHz，每个信号周期能够提供20个样本。虽然您可以使用本文介绍的方法进行更高倍数的上采样，但为了说明起见我们还是使用M=4的上采样。

当然，还可以通过直接在ADC生成的数据序列的每个实际样本值之间插入(M-1)个零来获得上采样数据向量及所需的样本数(公认效果较差)。该“零插入步骤”对应于复制频域中的原始信号频谱。通过对得到的“零填充”时域信号进行低通滤波，就能去除频域中所需频谱的“复本”，从而获得上采样数据向量。

FIR滤波器设计

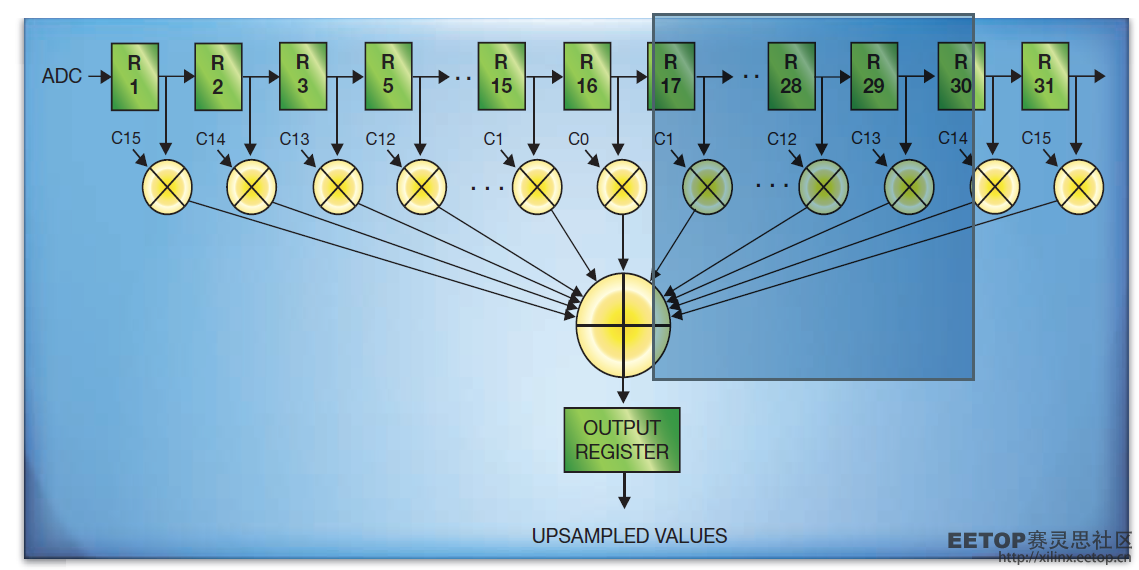
频域中的理想(砖墙式)低通滤波器相当于在时域中用无限域Sinc函数作卷积。因此为近似化所需的卷积运算，可让前述的零填充时域信号通过速率为ADC时钟频率M倍的对称低通FIR滤波器，该滤波器拓扑结构与图3所示的示例31抽头FIR滤波器相同。用这种方法，我们可以实时生成上采样数据向量。图3中的R1、R2、...、R31代表速率为ADC时钟频率M倍的寄存器，C0、C1、…、C15代表FIR滤波器的系数。

需要说明的是，图3所示的FIR滤波器中的大部分寄存器在任何特定时钟间隔内都会包含0，而非实际的样本数据。以M=4为例，当R1包含实际样本数据时，R2、R3和R4将包含0。当R1包含实际样本数据时，R5、R9、R13、R17、R21、R25和R29也将包含实际样本数据，其余的寄存器将包含0。在下一时钟间隔中，R2、R6、R10、R14、R18、R22、R26和R30将包含实际样本数据。

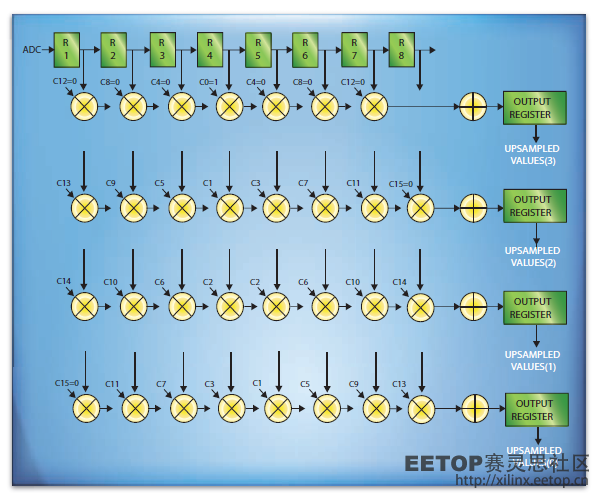
如图3所示，由于在通过FIR滤波器的每M个样本中有M-1个样本为0，就M=4、使用31抽头FIR滤波器的情况而言(如图4所示)，您可以将滤波器分解开，并行产生M个输出。采用这种实现方案，并行FIR滤波器的工作频率为ADC的基本时钟频率，而非ADC时钟频率的M倍。

如图4所示，您可以设定窗口SINC函数的系数Cw(n)来最大限度地减少实现该FIR滤波器所需的乘法器数量。对于T个抽头的低通FIR滤波器而言，可通过下式得出最佳系数：

等式2

这里的汉宁窗系数的计算方法为：

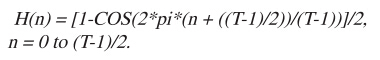
等式3

窗口SINC函数系数Cw(n)随即通过对应的C(n)和H(n)值相乘即可得到，如：

等式 4

在M=4时，如果按上面介绍的方法计算31抽头FIR滤波器的系数，令C0=1.0，C4=C8=C12=C15=0，则无需使用与图4中这些系数有关的9个乘法器。此外，由于生成UPSAMPLED VALUE(1)每个系数会使用两次，用户可以“折叠”该实现方案，比如在相乘之前让R1和R8相加，这样就可以去掉四个乘法器。最后得到的设计仅使用18个乘法器每时钟周期就可产生四个上采样值。需要注意的是按上文介绍的设计方法，每个原始样本值会原样从并联滤波器输出。

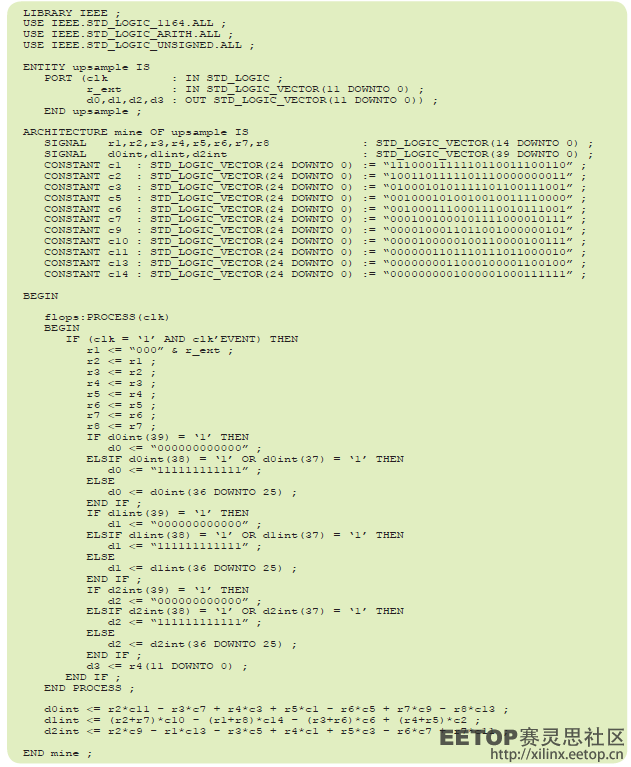
我们使用图5所示的可综合VHDL[5]模型评估图4所示电路的性能。该VHDL实现方案假定样本数据为12位，即可能来自美国模拟器件公司的AD9670八通道超声前端集成电路[6]的数据。滤波器系数表达为25位定点常数，以与集成到FPGA芯片上的乘法器输入位数相匹配。来自ADC的输入样本先馈入与输入引脚相连的寄存器(图4中的R1)，上采样输出值则使用与输出引脚相连的寄存器。寄存器R2到R8属芯片内部寄存器。寄存器R1到R8故意设定为15位宽度，以便为综合后逻辑提供执行计算所需的动态余量。该设计能检查溢出或下溢，还能将结果钳制在有效范围以内。

无需流水线化

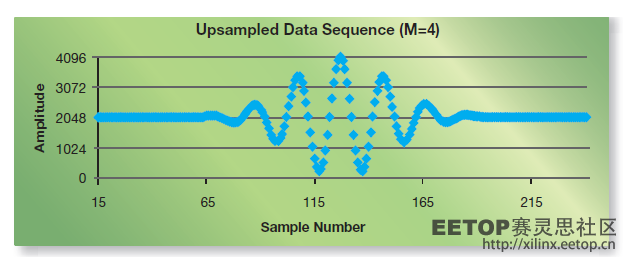
图6显示的是使用免费的赛灵思WebPACK™工具[8]中提供的14.7版ISim仿真器对该VHDL模型进行仿真并将馈送图2中的采样/量化12位数据序列后得到的上采样数据序列。每个原始的12位样本均保持不变，原因上文已述。原始波形中每个实际样本之间插入了三个新样本。

计算所得(上采样所得)值与原始模拟信号中理想值之间最大的误差为整个范围的0.464%，平均误差为整个范围的0.070%。当然因初始量化步骤原因，在采样/量化12位源矢量数据值中存在1/2 LSB的误差(合整个范围的0.012%)。

布局布线设计使用19个DSP48E1模块，但占用的Virtex-6 Slice资源不足1%，无需流水线化即可运行在107MHz下。

我们使用WebPACK工具14.7版在赛灵思XC6VLX75T-3FF484 Virtex-6 FPGA[7]上实现这一上采样器。布局布线设计占用该器件中288个DSP48E1模块中的19个，但使用的Slice资源不足1%。最终得到的上采样电路能够运行在107MHz下。无需让滤波器流水线化即可实现这一性能。此外，我们还开发出了用流水线实现的版本，可以工作在217MHz以上。

虽然XC6VLX75T-3FF484是赛灵思Virtex-6系列中的最低端成员，但芯片上仍集成有288个带有25x18位乘法器的DSP48E1模块。换言之，在理论上足以实现15个图4所示的并行上采样FIR滤波器。我们制作的原型环形阵列超声系统使用了八套以80MHz的频率运行在XC6VLX75T FPGA上的上采样器，在波束成形之前对来自八通道Analog Devices AD9670超声前端芯片的数据进行上采样处理。在该系统中，上采样器按仿真预测的方式运行，在以AD9670 ADC的基本时钟频率80MHz运行的情况下，能使用上采样到320MHz的数据实时完成波束成形。

最大型赛灵思Virtex-6 FPGA器件XC6VSX475T包含有2,016个25x18位乘法器，在理论上一个芯片就可以实现106个图4所示类型的上采样滤波器。

只要滤波器使用本文介绍的高效并行拓扑结构进行设计，就能够使用实现在工作频率为107MHz的赛灵思XC6VLX75T-3FF484 FPGA上的FIR滤波器完成M=4倍的实时上采样。原始数据样本将原封不动通过滤波器，并行产生(M-1)=3个上采样值。这种简明的FIR滤波器设计方法无需借助复杂精密的滤波器设计工具就能提供优异的结果。本文介绍的思路稍加拓展，就可以使用更大的因数进行上采样，或者是使用抽头数更多的FIR滤波器降低计算出的上采样值的误差。

这种简明的FIR滤波器设计方法无需借助复杂精密的滤波器设计工具就能提供优异的结果。

参考资料：

1. A.V. Oppenheim、R.W. Schafer，《离散时间信号处理》，Prentice Hall，新泽西州恩格尔伍德克利夫斯，1989年。

2. H. Stark、J.W. Woods、I. Paul，《使用直接傅里叶逆转换和最优插值法对计算机体层摄影术进行探讨》，IEEE生物医学工程通讯第28期，496到505页(1981年)。

3. R.W. Schafer、L.R. Rabiner，《插值的数字信号处理方法》，IEEE第61期会刊，692到702页(1973年)

4. R. Crochiere、L.R. Rabiner，《多速率数字信号处理》，Prentice Hall，新泽西州恩格尔伍德克利夫斯，1983年。

5. D. Pellerin、D. Taylor，《轻松VHDL设计》，Prentice Hall，新泽西州恩格尔伍德克利夫斯，1997年。

6. Analog Devices AD9670八通道超声AFE及数字解调器产品说明书，Sp0修订版，美国模拟器件公司，2013年。

7. Virtex-6系列总览2.3版(DS150)，赛灵思公司，2011年。

8. ISE深入教程13.1版(UG695)，赛灵思公司，2011年。