机器学习：朴素贝叶斯--python

今天介绍机器学习中一种基于概率的常见的分类方法，朴素贝叶斯，之前介绍的KNN, decision tree 等方法是一种 hard decision，因为这些分类器的输出只有0 或者 1，朴素贝叶斯方法输出的是某一类的概率，其取值范围在 0-1 之间，朴素贝叶斯在做文本分类，或者说垃圾邮件识别的时候非常有效。

朴素贝叶斯就是基于我们常用的贝叶斯定理：

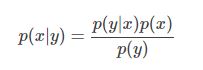
假设我们要处理一个二分类问题： c1,c2，给定一个样本，比如说是一封邮件，可以用向量 x 来表示，邮件就是一个文本，而文本是由单词构成的，所以 x 其实包含了这封邮件里出现的单词的信息，我们要求的就是，给定样本 x ，我们需要判断这个样本是属于 c1 还是属于 c2，当然，我们可以用概率表示为：

这个就是我们常见的后验概率。根据贝叶斯定理，我们可以得到：

这就是我们说的朴素贝叶斯，接下来的就是各种统计了。

我们给出一个利用朴素贝叶斯做文本分类的例子：

首先建立一个数据库：
def Load_dataset():
postingList=[['my', 'dog', 'has', 'flea', \
'problems', 'help', 'please'],
['maybe', 'not', 'take', 'him', \
'to', 'dog', 'park', 'stupid'],
['my', 'dalmation', 'is', 'so', 'cute', \
'I', 'love', 'him'],
['stop', 'posting', 'stupid', 'worthless', 'garbage'],
['mr', 'licks', 'ate', 'my', 'steak', 'how',\
'to', 'stop', 'him'],
['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
classVec = [0, 1, 0, 1, 0, 1]
return postingList, classVec

接下来，我们建立一个字典库，保证每一个单词在这个字典库里都有一个位置索引，一般来说，字典库的大小，就是我们样本的维度大小：
def Create_vocablist(dataset):
vocabSet = set([])
for document in dataset :
vocabSet = vocabSet | set(document)
return list(vocabSet)

我们可以将样本转成向量：一种方法是只统计该单词是否出现，另外一种是可以统计该单词出现的次数。
def Word2Vec(vocabList, inputSet):
returnVec = [0] * len(vocabList)
for word in inputSet :
if word in vocabList :
returnVec[vocabList.index(word)] = 1
else:
print ("the word %s is not in the vocabulary" % word)
return returnVec

def BoW_Vec(vocabList, inputSet):
returnVec = [0] * len(vocabList)
for word in inputSet :
if word in vocabList :
returnVec[vocabList.index(word)] += 1
else:
print ("the word %s is not in the vocabulary" % word)
return returnVec

接下来，我们建立分类器：这里需要注意的是，由于概率都是 0-1 之间的数，连续的相乘，会让最终结果趋于0，所以我们可以把概率相乘转到对数域的相加：
def Train_NB(trainMat, trainClass) :
Num_doc = len(trainMat)
Num_word = len(trainMat[0])
P_1 = sum(trainClass) / float(Num_doc)
P0_num = np.zeros(Num_word) + 1
P1_num = np.zeros(Num_word) + 1
P0_deno = 2.0
P1_deno = 2.0
for i in range(Num_doc):
if trainClass[i] == 1:
P1_num += trainMat[i]
P1_deno +=sum(trainMat[i])
else:
P0_num += trainMat[i]
P0_deno += sum(trainMat[i])
P1_vec = np.log(P1_num / P1_deno)
P0_vec = np.log(P0_num / P0_deno)

return P_1, P1_vec, P0_vec

def Classify_NB(testVec, P0_vec, P1_vec, P1):
p1 = sum(testVec * P1_vec) + math.log(P1)
p0 = sum(testVec * P0_vec) + math.log(1-P1)
if p1 > p0:
return 1
else:
return 0

def Text_parse(longstring):
import re
regEx = re.compile(r'\W*')
Listoftokens = regEx.split(longstring)
return [tok.lower() for tok in Listoftokens if len(tok)>0]
# return Listoftokens

这里给出简单的测试：
test_string = 'This book is the best book on Python or M.L.\
I have ever laid eyes upon.'

wordList = Text_parse(test_string)

Mydata, classVec = Load_dataset()

'''
Doc_list = []
Full_list = []
for i in range (len(Mydata)):
Doc_list.append(Mydata[i])
Full_list.extend(Mydata[i])
'''

Vocablist = Create_vocablist(Mydata)

Wordvec = Word2Vec(Vocablist, Mydata[0])

trainMat = []
for doc in Mydata:
trainMat.append(Word2Vec(Vocablist, doc))

P_1, P1_vec, P0_vec = Train_NB(trainMat, classVec)

print Mydata
print classVec
print wordList