基于DDS的椭圆函数低通滤波器的设计

     摘要：低通滤波器是直接数字频率合成DDS的重要组成部分，其性能的好坏直接影响整个DDS的特性。提出一种基于DDS的椭圆函数低通滤波器的设计方案，该设计采用全新的归一化方法，并使用EDA软件Multisim2001进行仿真，确定了滤波器的结构，阶数，以及设置了相关参数，从而设计出截止频率为160 MHz的7阶椭圆函数滤波器。该低通滤波器幅频特性良好，具有快速的衰减性。因此该设计方案可适用于不同频段、阶数、类型的滤波器设计。

　　直接数字频率合成(DDS)技术是20世纪70年代以来推出的一种频率合成法。随着数字集成电路和微电子技术发展，DDS技术已广泛应用于电子、通信、雷达等领域。DDS是通过改变频率控制字来改变相位累加器的相位累加速度，在固定时钟的控制下取样得到相位值，由相位幅度转换得到相位值对应的幅度序列，该幅度序列再通过数模转换及低通滤波后得到模拟的正弦波输出。

　　由于DDS自身的结构特点，其输出信号中含有大量的杂散谱线，产生杂散的主要原因：1)相位截断误差效应；2)存放ROM中的正弦波幅度量化误差；3)D／A转换器的非理想特性。在整个DDS的实现过程中，低通滤波器除了滤除上述的高频信号以外还有去除杂散的作用，因此，低通滤波器的滤波特性的好坏直接影响整个DDS的技术指标。

　　1 低通滤波器

　　理想的滤波电路通带内具有最大幅值和线性相移，阻带内幅值为零，但是实际滤波电路往往难以达到理想特性，设计时只能根据具体需要，寻求最佳方案，得到近似理想的滤波电路。滤波器可以分为模拟和数字滤波器，模拟滤波器又可以分为无源和有源两种。一个滤波器是用一组输入输出对儿或激励一响应对儿表征的系统。滤波器的性能用一些参数来表征，最常用的技术参数是频率响应，称传递函数。根据传递函数的形式，比较普遍的滤波器有巴特沃斯滤波、切比雪夫滤波和椭圆滤波等。图1为3种滤波器的幅频特性的比较。

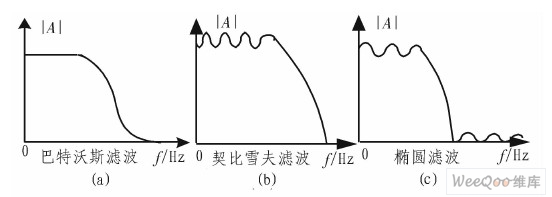
图1 3种滤波器的幅频特性的比较

　　图1(a)为巴特沃斯滤波器的幅频特性曲线，其通带和阻带是平坦的，但是其过渡带太过平缓；图l(b)为契比雪夫低通滤波器的幅频特性曲线，其通带是等波纹抖动的，阻带内衰减单调增大，仅在无限大阻带处衰减为无限大，过渡带比巴特沃斯滤波器稍稍陡峭；图l(c)为椭圆函数滤波器的幅频特性曲线，其通带和阻带都是抖动的，但其过渡带下降迅速，过渡带很窄。相比椭圆函数滤波器的性能较好。

　　2 低通滤波器的设计

　　根据DDS原理，频率控制字K和时钟频率f共同决定DDS的输出频率fo，它们之间满足(N为相位累加器的位数)。由奈奎斯特采样定理，输出的最高频率是DDS的时钟频率fs的50％(理论值)，但是考虑到低通滤波器的设计难度以及对输出信号杂散的抑制，实际频率只达到40％fs。

　　AD9954高集成度频率合成器工作时钟可达400 MHz，该滤波器是建立在AD9954基础上，由采样定理可知，AD9954输出的最高频率为200 M-Hz，则该低通滤波器的截止频率为200 MHz。

　　2．1 低通滤波器的设计方案

　　设计一个滤波器，首先必须考虑滤波器的幅频特性、电路输入、阻抗匹配、截止频率等参数，根据设计参数确定具体曲线和归一化的元件值，然后根据去归一化得到实际元件值。

　　椭圆函数滤波器的幅度函数为：

　　要设计一个滤波器，首先必须根据给定的通带最大衰减A。或ρ(通带边界上的反射系数)，阻带最小衰减As，选择性因子k确定所要求的阶数N。在实际应用中，一般都选择fp为基准频率，在这种情况下，通带上限频率和阻带下限频率的归一化值分别为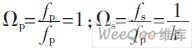，选择性因子k就是与椭圆函数滤波器有关的各椭圆函数的模数。在椭圆函数理论中，k=sinθ表示模数k，θ称为模角。由于这4个参数的关系相当复杂，用解析法求解阶数很困难，可用特制的图表确定阶数N。

　　2．2 滤波器阶数的确定

　　本文设计的椭圆函数滤波器：截止频率为160 MHz；通带内起伏量为0．1 dB；阻带频率为200 MHz，此处的最小阻带衰减为50 dB；特性阻抗：R1=R2=200 Ω。

　　首先根据文献估算椭圆函数滤波器阶数用的曲线，并由给定的技术指标(阻带频率Ωs，反射系数ρ，阻带最小衰减As)估算滤波器的阶数N。

　　1)根据设计要求可得低通陡度系数；

　　2)根据阻带端点Ωs内的最小阻带衰减为50 dB，由文献中Rdb，ε，ρ之间的关系，获得该设计要求的通带起伏量为0．1 dB，从而计算出反射系数ρ=15％；

　　3)查找估算阶数曲线得到Aρ=16．5，则Aρ+Amin=66．5；

　　4)查找文献，在Ωs=l．25时，N=7可满足给定的衰减量。因N为奇数，所以模数k和模角θ可直接由Ωs求得：k=1／Ωs=1／1．25=0．8，θ=sin-1k=53．13°。实际采用θ应较该数值略大，以便超过裕量。在N=7时，选取0=55°。可得 Ωs=1．220 8。由该截止Ωs值可求出实际截止频率：fc=fs／Ωs=200／1．220 8=163．83 MHz。

　　2．3 归一化设计及仿真结果

　　归一化低通滤波器是指特性阻抗为1Ω且截止频率为1／(2π)Hz的滤波器。归一化的方法是首先通过改变归一化低通滤波器的元件参数值，得到一个截止频率从归一化截止频率1／(2π)Hz变为待设计滤波器所要求截止频率而特性阻抗等于归一化特性阻抗1 Ω的过渡性滤波器；然后再通过改变这个过渡性滤波器的元件值，把归一化特性阻抗1 Ω变成待设计滤波器所要求的特性阻抗，从而最终得到所要设计的滤波器。其具体步骤如下：

　　1)确定归一化数据 7阶椭圆型低通滤波器的模型见图2，其中X1，X2，X4，X5，X7，X8，X10为电容，X3，X6，X9为电感。依据参考文献中提供的各个元件的归一化数据来设计相应的电容电感大小。表1为7阶带内起伏量为0．1 dB，阻带频率倍数为1．25的归一化数据表，表中的电容单位为F，电感单位为H。

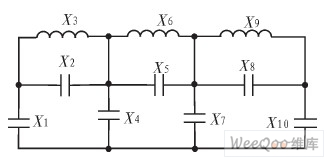
图2  7阶椭圆型低通滤波器的模型

表1 椭圆型低通滤波器设计数据

　　2)截止频率变换 得到了截止频率为160 MHz，特性阻抗等于归一化特性阻抗1 Ω的过渡性滤波器。对归一化元件参数进行如下变换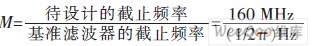：，电感变换L(MID)=L(OLD／M；电容变换C(MID)=C(OLD)／M。将表l中的归一化数据转化为过渡数据，如表2所示，其中截止频率160 MHz，特性阻抗1 Ω。

表2 7阶椭圆型低通滤波器元件参数

　　3)阻抗变换 由过渡性滤波器转换成最终需要的截止频率为163．83 MHz，特性阻抗为200 Ω的滤波器。过渡性元件参数变换如下：K=待设计滤波器特性阻抗／基准滤波器特性阻抗=200 Ω／1Ω=200；电感变换L(NEW)=L(MID)K；电容变换C(NEW)=C(MID)／K。

　　根据所需滤波器各元件的参数，如表3所示，其中截止频率160 MHz，特性阻抗200 Ω。根据变换之后的元件参数值得到的椭圆函数滤波器仿真电路见图3，Multisim2001仿真结果如图4所示。

表3 7阶椭圆型低通滤波器元件数据

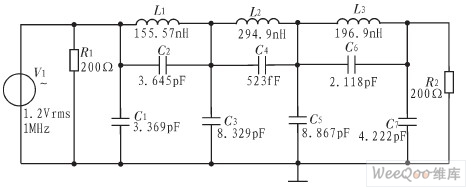
图3 仿真电路图

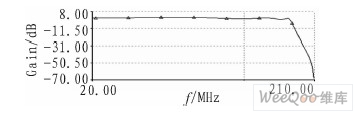
图4  Multisim2001仿真结果

　　从Multisim2001仿真结果来看，整体幅频特性良好，仅在150 MHz附近有少许衰减，假如衰减量不在允许范围内，可在滤波器的最后加上电路补偿部分，补偿的原则是使得幅度值在高频处有一定的增大。

　　3 结论

　　设计的滤波器阶数为7阶，截止频率为160 MHz，具有良好的幅频特性和快速的衰减速率，在200 MHz处衰减为66．5 dB。对高频信号的滤波作用明显，输出信号特性好，利用该设计方法可设计各频段的低通滤波器。