杨超,钱慧
(福州大学 物理与信息工程学院,福建 福州 350108)
摘要:提出了一种基于最优搜索的稀疏傅里叶变换(SFT)的并行实现设计。首先将输入信号分为并行N组,分别进行快速傅里叶变换(FFT),实现信号频率分量的取模处理,然后通过排序搜索获得。经验证,相较于FFTW,当信号长度大于524 288时,执行时间会有更好的表现;相较于正交匹配算法及其他SFT的FPGA实现,其系统的复杂度降低了。
关键词:稀疏傅里叶变换;并行框架;现场可编程门阵列
中图分类号:TN911.7文献标识码:ADOI: 10.19358/j.issn.1674-7720.2017.10.020
引用格式:杨超,钱慧.面向FPGA的稀疏傅里叶并行算法实现[J].微型机与应用,2017,36(10):70-73.
0引言
稀疏傅里叶变换(Sparse Fourier Transform, SFT)是一种新的算法框架,也是快速傅里叶变换(Fast Fourier Transform,FFT)在处理稀疏频谱信号上的延伸。2003年AYDINER A A等人提出了针对频域稀疏信号的傅里叶变换基本思想[1]。对于频域稀疏信号来说,其频谱可以通过其多级子集频谱获得。之后,IWEN M A等人从压缩感知得到启发,将采样和频率估计整合到快速傅里叶变换并提出了经典SFT框架[2]。之后SFT广泛运用于稀疏频谱信号(诸如音频信号、医学图像信号)的处理以及频谱感知领域[3]。大量的SFT算法被提出,它们多利用经典的频率估计算法通过亚奈奎斯特采样点的子集的傅立叶变换重构稀疏频点[4]。但由于经典SFT的亚奈奎斯特率样本是通过多次采样获得的,因此,经典SFT 不可能代替 FFT来处理实时信号,比如雷达信号等。
2010年以来,一种并行结构的SFT算法受到了广泛的关注[5]。并行SFT首先通过并行下采样,采集计算所需的所有时域数据,然后再通过FFT,通过亚线性频谱估计方法获得信号的稀疏频率及其幅值。由于该类方法以并行取代迭代获得频谱估计所需的所有信息,因此可以实时处理各种频域稀疏信号,使得经典SFT得到了改善。基于此,参考文献[6]~[8]探讨了稀疏傅里叶变换在GPU以及多核CPU上的实现方式。这些研究显示,基于GPU加速的实现方案运行速度要显著高于基于CPU的实现方案。然而,基于GPU的实现方案都存在主存储区与GPU存储区的连接交互问题,因此数据间的正常流动不能得到更好的促进。
为解决GPU的数据并行处理的局限性,本文研究SFT的并行算法并在FPGA上对其进行实现,同时应用中国余数定理(CRT)的基本原理对信号进行重构。相较于传统的SFT,本文的方法可以极大地降低系统的复杂度,减少了硬件的开销。本文,首先介绍SFT的并行框架,然后讨论SFT的FPGA实现架构,最后从仿真结果以及硬件实现两方面对系统进行评估。
1SFT并行算法
SFT并行算法主要由下采样、频率估计、幅度估计三个部分组成。在下采样过程中,将输信号划分为N个组,每个组的采样因子分别为σ1,σ2,…,σN。利用中国余数定理(Chinese Residue Theorem,CRT)进行频率以及幅度的估计,设定各组的采样因子两两互质。
并行SFT算法从L个采样样点中重构2 K算个参数,其中包括K个时延参数以及K个幅度参数。重构法的具体计算步骤如下:首先,设采样通道数为N,每个通道的采样点数分别为qi,i=1,2,…,N。计算X~=M*X,其中M为下采样矩阵,X为采样样本。之后,对X~进行DFT变换,得到X^=DFT(X~)。按幅度从大到小对X^向量中的值进行排序,计算hk:
hk=kthMAX|X^j|,k∈[0,K](1)
其中K为指定的重构信号的参数。得到hk之后则可通过求余运算获取余数信息r1,k?hk的位置modq1。通过并行查询的方式搜索余数的最优解:
tmin?mint∈[0,qj]|hk-X^t*q1+r1,k|,j∈[2,N](2)
rj,k=r1,k+tmin*q1modqj,j∈[2,N](3)
利用CRT通过r1,b,…,rN,b重构时延参数τk,幅度估计参数可由公式(4)和 (5)得出:
x=real(hk)|τk
y=imag(hk)|τk(4)
ak=|x+iy|(5)
2SFT主要部分的FPGA实现
本文考虑使用MATLAB?Simulink工具构建SFT采样算法的FPGA实现架构。图1展示了当采样通道数N=3时的SFT并行结构,其主要包括下采样、频率估计、幅度估计三个部分。
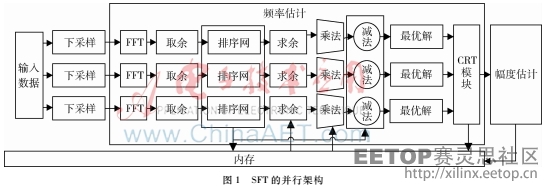
如图1所示,频率估计与幅度估计共用部分相同的硬件结构,信号在经过下采样之后,通过FFT运算得到复数的输出信号,为了对该复数信号进行排序,将该复数信号取模后送入排序网络,由于每个通道送入排序网络的点数不同,排序网络的结构会稍有差异。在利用CRT估计信号的幅度和频率之前,需要对信号进行求余、求最优解等运算。其中,最优解运算的核心是排序网络,利用排序网络的思想求取输入信号的最大值以及获取排序后的信号在原输入信号中的位置;CRT模块由一些加法器和乘法器组成。
输入信号经过多路选择器获得下采样信号,所以该部分主要研究下采样信号的频率估计以及幅度估计,频率估计包括最优解模块以及CRT重构模块。另外,硬件构成部门还包含了存储和控制单元,各通道采样因子数ql、参数t、排序位置信息等都在存储单元中保存,控制单元产生地址值来执行读写存储器的操作,并输出必要的控制信号来初始化运算模块。
在本设计中,设定信号长度N=223,参数个数K,采样通道数M=3,其中,各个通道的采样点分别为q1,q2,q3;q1,q2,q3两两互质且乘积大于信号长度N,因此,通过中国余数定理可由q1+q2+q3个采样点数获取原始信号所有的信息,降低了幅度以及频率估计时所需的采样点数。下面介绍各个主要功能模块的设计。
2.1频率估计
2.1.1最优解模块实现架构
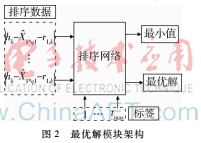
频率估计模块的核心部分在于最优解的获得,最优解实现架构如图2所示。图中X^t*q1+r1,k可由采样样本经过多路选择器MUX获得,根据t的取值不同,可以得到多个定点采样的样点值。当排序网络为三输入结构时,r1,k代表排序网图2最优解模块架构络模块中获得的k1,1,k1,2,k1,3对应位置信息数据对q1取余所得的值。t的取值范围为0~qj,j=2,3,其中当j=2时,q2=4,同样地,有q3=5;两种情况下只有t值的变化导致定点采样的样点值的变化,而其对应的模块架构是相同的,所以这里仅对j=2时的情况加以分析。
根据排序网络结构,需要的输入数据有两组,一组为需要排序的数据,以便求得最小值,另外一组则为数据对应的位置信息t。这样在排序网络求取完最小值后可以直接获取相应的t值而不需要进行其他的运算处理。为此,将需要排序的数据并行导入排序网络的数据输入接口,将对应的位置信息t值也并行导入排序网络的位置信息接口。
如图3所示,原有输入的3路信号序号为1,2,3。该模块实现对这3路信号进行从大到小的排序,并获得排序后的信号在原序列中的序号,即取位。图3显示了3输入结构的排序图,4输入乃至更多输入结构图原理相同,图中比较器的输出作为多路选择器的sel选择端输入,利用比较器以及多路选择器的硬件电路连接实现逻辑上的比较选择排序。k1,1,k1,2,k1,3为3输入信号经过排序网络的输出信号,有k1,1>k1,2>k1,3。k1,1_loc,k1,2_loc,k1,3_loc分别记录了k1,1,k1,2,k1,3在原序列中的位置。同时将位置信息存储到位置信息存储器中。

2.1.2CRT模块架构
最优解模块输出一组余数信息的集合,利用中国余数定理可以轻易地通过一组累加求和运算获取频率集合,进一步便可获取时延参数τk。由中国余数定理可以得到如下方程组:
x≡r1(modq1)
x≡r2(modq2)
?
x≡rn(modqn) (6)
其中ri(i=1,2,…,n)为频率点的集合,qi(i=1,2,…,n)为采样点数的集合。假设Q为q1到qn的乘积,并设Qi=Q/qi,?i∈{1,2,…,n},ti为Qi模qi的数论倒数,则有:
x=∑ni=1ritiQi(7)
图4显示了一个频率点的CRT重构模块架构。
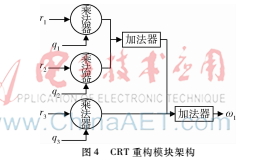
2.2幅度估计
幅度估计中,利用CRT重构模块中获取的频率集合w1,w2分别与L1,L2作求余运算,以此为基础求得hk,利用前面式(4)和式(5)可求得原始信号的幅度估计。其中频率集合w1,w2由CRT模块获得,图5中求余的作用为频率集合w1,w2分别对采样点数L1,L2作求余运算。输入序列xl、稀疏度值、采样通道数、每个通道的采样点数存储在寄存器中供乘法器调用。利用排序网络分别求得输入信号实部与虚部的最大值,再对其进行取模则可得到幅度值的估计。幅度估计的模型如图5所示,其中,排序网络为4输入结构。

3结果分析以及性能评估
为评估该算法框架的有效性,将其与FFTW做对比,FFTW是一个快速计算离散傅里叶变换的库,这个库可以在多核CPU以及GPU上运行。分别考虑稀疏度k恒定为1 000时信号长度的变化对执行时间的影响,以及信号长度N恒定为223时稀疏度的变化对执行时间的影响,比较结果如图6所示。
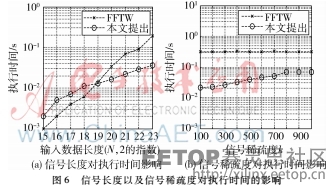
将本文讨论的稀疏傅里叶变换采样框架与已知的OMP算法框架作性能上的对比,实现了信号长度N=32,参数个数K=2以及采样点数的采样框架。其中,使用RAM块实现所有所需的向量、常数或矩阵的存储。将OMP架构[9]以及SFT架构[10]在同样的平台下做了实现来与本文算法架构进行对比,其结果如表1所示。
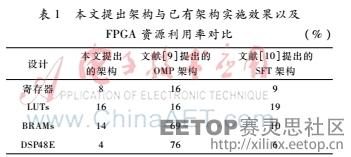
相较于OMP架构,本文提出架构大大减少了DSP48E以及所需寄存器的数量。相较于文献[10]提出的SFT架构,本文架构依旧能够有良好的表现。
4结论
本文提出了SFT的FPGA并行实现方案,使用Simulink中的XSG开发工具构建FPGA实现框架。对独立功能块的并行化处理可以大大减少执行时间。之后对FPGA上的硬件实现进行了评估,相对于FFTW的实现方案,在采样点数的量级足够大时,提高了系统运行速度,降低了计算所需的时间;相对于其他OMP等算法的FPGA实现方案,减少了资源的消耗,降低了系统的复杂度。
参考文献
[1] AYDINER A A, WENG C C, SONG J, et al. A sparse data fast Fourier transform (SDFFT)[J]. IEEE Transactions on Antennas & Propagation, 2003, 51(11):3161-3170.
[2] IWEN M A. A deterministic sub?linear time sparse Fourier algorithm via non?adaptive compressed sensing methods[C]. Proceedings of the nineteenth annual ACM?SIAM symposium on Discrete Algorithms, 2008: 20?29.
[3] 那美丽, 周志刚, 李霈霈. 基于稀疏傅里叶变换的低采样率宽带频谱感知[J]. 电子技术应用, 2015, 41(11):85-88.
[4] GILBERT A C, STRAUSS M J, TROPP J A. A tutorial on fast fourier sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 57-66.
[5] Wang Cheng, ARAYA?POLO M, CHANDRASEKARAN S, et al. Parallel sparse FFT[C].Proceedings of the 3rd Workshop on Irregular Applications: Architectures and Algorithms. ACM, 2013:10:1-10:8.
[6] Hu Jiaxi, Wang Zhaosen, Qiu Qiyuan, et al. Sparse fast Fourier transform on GPUs and multi?core CPUs[C].2012 IEEE 24th International Symposium on Computer Architecture and High Performance Computing (SBAC?PAD), IEEE, 2012: 83-91.
[7] BRAUN T R. An evaluation of GPU acceleration for sparse reconstruction[J]. Proceedings of SPIE?The International Society for Optical Engineering, 2010, 7697.
[8] Wang Cheng, CHANDRASEKARAN S, CHAPMAN B. cusFFT: a high?performance sparse fast fourier transform algorithm on GPUs[C].Proceedings of 30th IEEE International Parallel & Distributed Processing Symposium (IPDPS),2016:936-972.
[9] RABAH H, AMIRA A, MOHANTY B K, et al. FPGA implementation of orthogonal matching pursuit for compressive sensing reconstruction[J]. IEEE Transactions on Very Large Scale Integration Systems, 2015, 23(10): 2209-2220.
[10] AGARWAL A, HASSANIEH H, ABARI O, et al. High?throughput implementation of a million?point sparse Fourier Transform[C].IEEE Conference on Field Programmable Logic and Applications (FPL), 2014: 1-6.

本视频基于Xilinx公司的Artix-7FPGA器件以及各种丰富的入门和进阶外设,提供了一些典型的工程实例,帮助读者从FPGA基础知识、逻辑设计概念

本课程为“从零开始大战FPGA”系列课程的基础篇。课程通俗易懂、逻辑性强、示例丰富,课程中尤其强调在设计过程中对“时序”和“逻辑”的把控,以及硬件描述语言与硬件电路相对应的“

课程中首先会给大家讲解在企业中一般数字电路从算法到流片这整个过程中会涉及到哪些流程,都分别使用什么工具,以及其中每个流程都分别做了
@2003-2020 中国电子顶级开发网